2021年国家公务员考试每日一练：数量关系（24）

　　9月18日更新的2021年国家公务员考试每日一练是数量关系题，多做公务员考试模拟题练习不仅有利于掌握考点，而且能够帮助保持题感，潜移默化中熟悉命题规律，提高公务员考试做题准确率。

　　1、某项工程，若王强单独做，需40天完成；若李雷单独做30天后，王强、李雷再合作20天可以完成。如两人合作完成该工程，王强第一天工作但每工作一天休息一天，问整个工程将会在第几天完成（ ）

　　A、44

　　B、45

　　C、46

　　D、47

　　2、A、B两船在静水中的航行速度分别为江水中水流速度的3倍和5倍。B船8点从上游的甲码头出发全速行进，中午11点到达下游的乙码头后原路返回。10点30分时，A船也从甲码头出发向乙码头全速行进。问两艘船相遇的点到甲码头和乙码头距离之间的比为：（  ）

　　A、5:4

　　B、7:6

　　C、3:2

　　D、4:3

　　3、英语课上，每位同学都要轮流做汇报，前一位同学做完汇报后，要让大家休息3分钟之后下一位同学才开始汇报，已知前三位同学汇报完共花了21分钟，假设每位同学的汇报时间相同，那么10位同学都汇报完需要多少分钟？（  ）

　　A、70

　　B、77

　　C、80

　　D、90

　　4、有一座长900米的大桥，A以1米/秒的速度从桥的一端步行过桥，过了10分钟后B骑自行车去追，假设正好在桥的另一头追上，则B的速度为（  ）米/秒。

　　A、1.5

　　B、2

　　C、2.5

　　D、3

　　5、有6个相同大小的容器，其中4个装水，有2个装了酒精。如果用天平称出哪两个容器中装的酒精，最简便的方法下能保证在第几次称重时发现？（　）

　　A、6次

　　B、5次

　　C、4次

　　D、3次

　　【下面是参考答案与解析。如果你认为题目或解析有误，可点这里给我们纠错。】

　　1、B

　　第一步：分析问题

　　本题是工程问题，工作总量一定，根据公式：工作效率=工作总量/工作时间，根据题目条件求出工作效率，即可最后求得工作时间。

　　第二步：计算过程

　　“若王强单独做，需40天完成；若李雷单独做30天后，王强、李雷再合作20天可以完成”即：王强40天工作量=李雷50天工作量+王强20天工作量，所以王强20天工作量=李雷50天工作量，则王强李雷二人效率比为5:2。

　　赋值王强的效率为5，李雷的为2，则工作总量为5×40=200。“两人合作完成该工程，王强第一天工作但每工作一天休息一天”，那么两天两人完成5+2+2=9的工作量，200/9=22余2，即44天后还剩2的工作量没有完成，还需要一天，所以整个工程将会在第45天完成。

　　故正确答案为B。

　　2、A

　　第一步：分析问题

　　本题可以设未知量水流速度，根据水流速度和A、B船在静水中的速度的关系，求出船速，根据公式：路程=速度×时间，结合题目条件可以求出两船到甲、乙码头的距离之比。

　　第二步：计算过程

　　赋值水速为1，则A、B两船在静水中的速度分别为3和5。甲码头在上游，所以从甲码头到乙码头为顺流，反之为逆流。B船用3小时从甲码头到达乙码头，所以两码头之间的距离为(5+1)×3=18；而11点时，A船离开甲码头半小时，距离乙码头18-(3+1)×0.5=16,从11点开始到两船相遇，设所需时间为t，则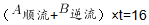，即(3+1+5-1)×t=16，解得t=2。此时B船距离乙码头(5-1)×2=8，距离甲码头18-8=10，所以相遇点到甲乙码头的距离比为10:8=5:4。

　　故正确答案为A。

　　3、B

　　解析：前三位同学汇报完成时，共休息两次为6分钟，则每名同学汇报时间为分钟。10位同学汇报完成共需休息10-1=9次，汇报完需用时5×10+9×3=77分钟。

　　故正确答案为B。

　　4、D

　　解析：桥全长900米，A速度为1米/秒，即60米/分，则A走完全程需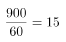分钟。B在A出发10分钟后开始追赶，两人同时到达，则B走完全程用时为15-10=5分钟，B速度为。

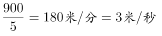　　故正确答案为D。

　　5、D

　　解析：酒精的密度比水小，所以相同容积的酒精比水质量小。先各取三个容器放置于天平两端，若天平平衡，则表明两个较轻的容器在天平两端各一个，此时从天平的一端任取两个称，就可确定那个较轻的容器，另一端同理称一次。若第一次操作之后，天平不平衡，则表明两个较轻的容器在天平较高的那一端，此时只需要从其中选出两个称一次，即可确定那两个较轻的容器。

　　综上所述，3次可以确保找出。